Colégio Estadual “Fausto Cardoso”
Disciplina: Matemática 2ª
unidade
Profª Elen Carla
2 º anos A, B e D
Aula 1
Vídeo para reforçar a aprendizagem
Matrizes
A matriz é
comumente utilizada para a organização de dados tabulares a fim de facilitar a
resolução de problemas. As informações das matrizes, sejam estas numéricas ou
não, são dispostas organizadamente em linhas e colunas.
O
conjunto das matrizes munido das operações de adição, subtração e multiplicação e
de características, como elemento neutro e inverso, forma uma estrutura
matemática que possibilita
sua aplicação em diversos campos dessa grande área do
conhecimento.
Representação de matrizes
Antes de
começarmos os estudos sobre matrizes, é necessário estabelecer algumas notações
quanto às suas representações. As matrizes são sempre representadas por
letras maiúsculas (A, B, C…), que são acompanhadas por índices, nos quais
o primeiro número indica a quantidade de linhas, e o segundo, o número
de colunas.
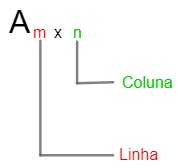
A quantidade
de linhas (fileiras horizontais) e colunas (fileiras
verticais) de uma matriz determina sua ordem. A matriz A
possui ordem m por n. As informações contidas em uma matriz são chamadas de elementos e ficam organizadas
entre parênteses, colchetes ou duas barras verticais, veja os exemplos:
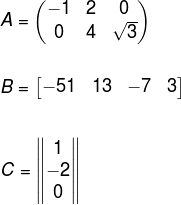
A matriz A possui
duas linhas e três colunas, logo, sua ordem é dois por três → A2x3.
A
matriz B possui uma linha e quatro colunas, logo, sua ordem é um por quatro,
por isso recebe o nome de matriz
linha → B1x4.
A
matriz C possui três linhas e uma coluna, e por isso é chamada de matriz coluna e
sua ordem é três por um → C3x1.
Podemos
representar genericamente os elementos de uma matriz, isto é, podemos escrever
esse elemento utilizando uma representação matemática. O elemento genérico será representado
por letras minúsculas (a, b, c…), e, assim como na
representação de matrizes, ele também possui índice que indica sua localização.
O primeiro número indica a linha em que o elemento está, e o segundo número
indica a coluna na qual ele se localiza.
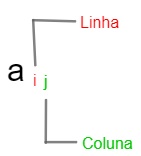
Considere a seguinte matriz A, faremos a
listagem de seus elementos.
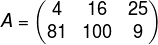
Observando o primeiro elemento que está
localizado na primeira linha e primeira coluna, ou seja, na linha um e coluna
um, temos o número 4. A fim de facilitar a escrita, vamos denotá-lo por:
a11 →
elemento da linha um, coluna um
Assim
temos os seguintes elementos da matriz A2x3:
a11 =
4
a12 =16
a13 = 25
a21 = 81
a22 = 100
a23 = 9
De modo geral, podemos escrever uma matriz em função de seus
elementos genéricos, essa é a matriz
genérica.
Uma matriz de m linha e n colunas
é representada por:
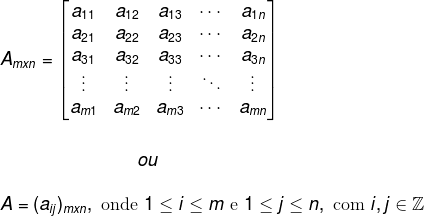
·
Exemplo
Determine a matriz A = [aij ]2x2, que possui
a seguinte lei de formação aij = j2 – 2i. Dos
dados do enunciado, temos que a matriz A é de ordem dois por dois, ou seja,
possui duas linhas e duas colunas, logo:
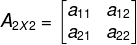
Além
disso, foi dada a lei de formação da matriz, ou seja, a cada elemento
satisfaz-se a relação aij = j2 – 2i.
Substituindo os valores de i e j na fórmula, temos:
a11 = (1)2 - 2(1) = -1
a12 = (2)2 - 2(1) = 2
a21 = (1)2 - 2(2) = -3
a22 = (2)2 - 2(2) = 0
Portanto, a matriz A é:
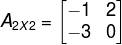
Atividade Remota 1

